蝴蝶定理公式大全(蝴蝶定理及四种平面几何证法简介)
蝴蝶定理(Butterfly Theorem):如图1,MN是圆O的弦,过MN的中点A任作两弦BC、DE,设CD、EB分别交MN于P、Q,则A为PQ的中点。
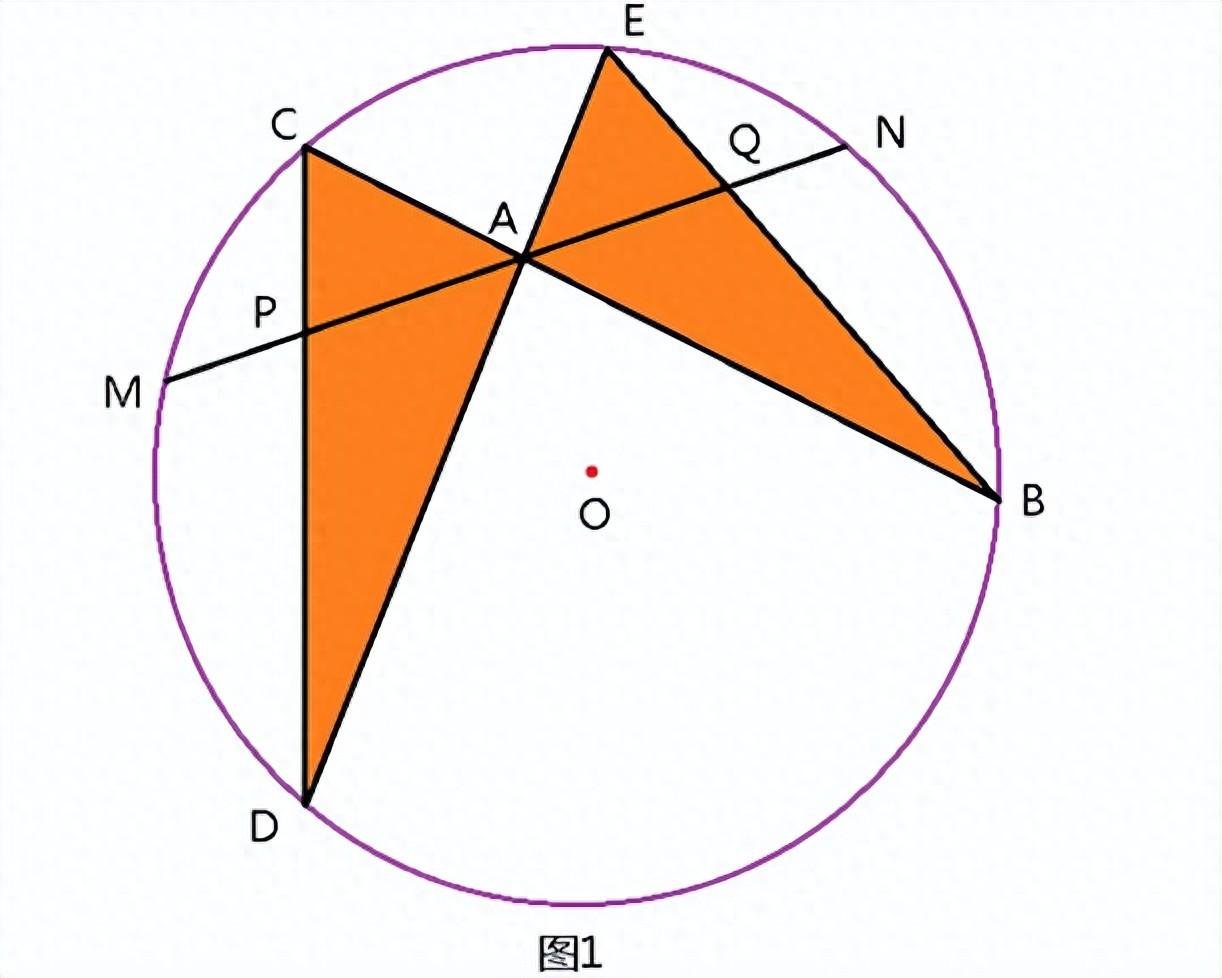
蝴蝶定理因其形似蝴蝶而得名,证明方法较多,本文介绍四种平面几何证法供大家参考。
- 霍纳证法
过点O作OF⊥CD,OG⊥EB,垂足分别为F、G,根据垂径定理得:CF=FD,EG=GB;
连接OP、OQ、AF、AG;连接OA,则OA⊥MN(图2)。
易证△CAD∽△EAB,则
AD/DC=AB/BE,因2DF=DC,2BG=BE,则AD/DF=AB/BG,
∠FDA=∠GBA=α,故△FAD∽△GAB,
∠AFD=∠AGB,∠AGQ=∠AFP(等角的补角相等)。
易证A、O、F、P和A、O、G、Q四点共圆,
∠AOP=∠AFP=∠AGQ=∠AOQ。
在Rt△AOP和Rt△AOQ中,
∠AOP=∠AOQ,AO=AO,则
Rt△AOP≌ Rt△AOQ,
AP=AQ,故A为PQ的中点成立。
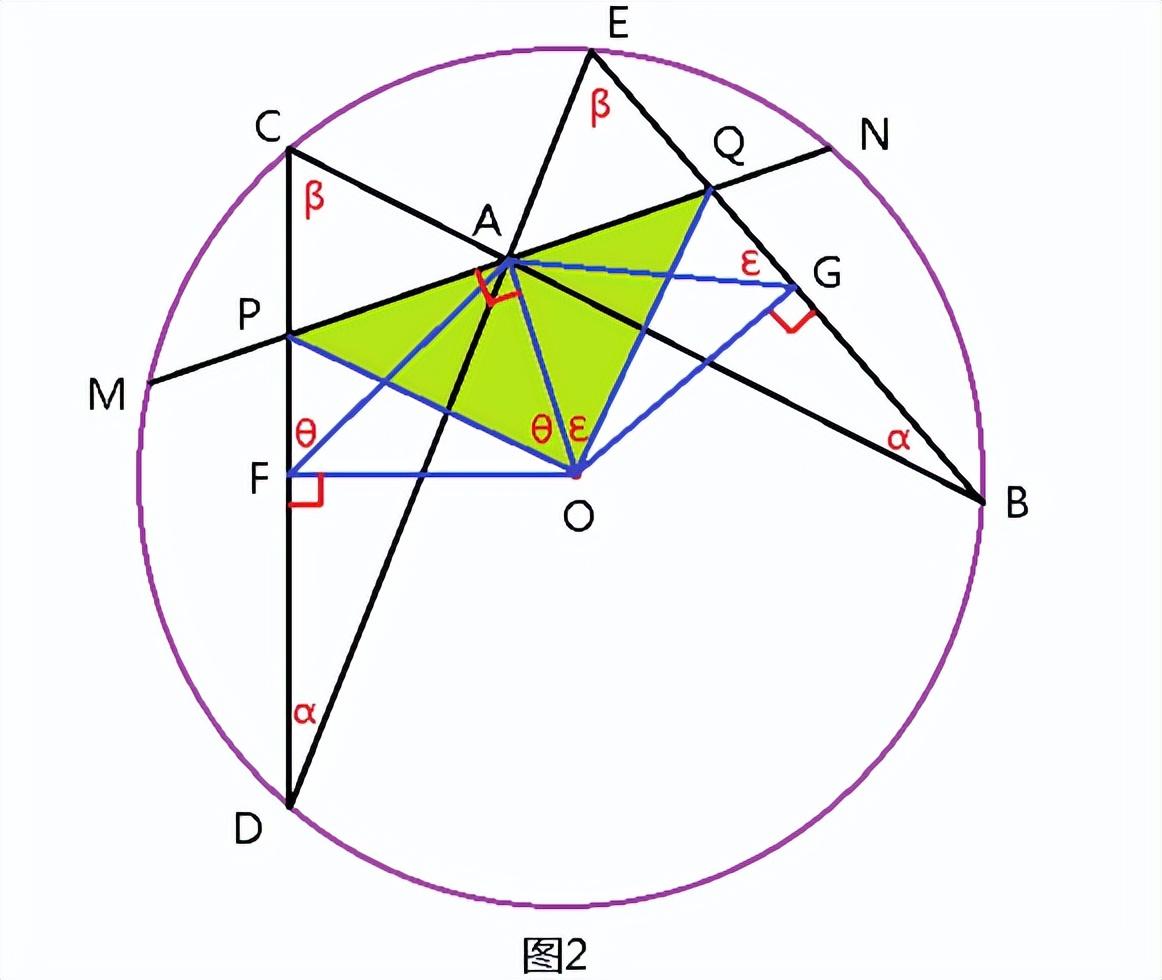
2.对称法
过点D作MN的平行线交圆于F(图3),连接AO并延长交DF于H,则AH为DF的垂直平分线,故
∠PAD=∠ADF=∠AFD=∠QAF=θ,AD=AF。
在圆内接四边形EDFB中,∠EDF+∠EBF=180°,即
∠QAF+∠EBF=180°,故Q、A、F、B四点共圆,则
∠CDE=∠CBE=∠AFQ=α。
易证△PAD≌△QAF,故PA=AQ,
A为PQ的中点得证。
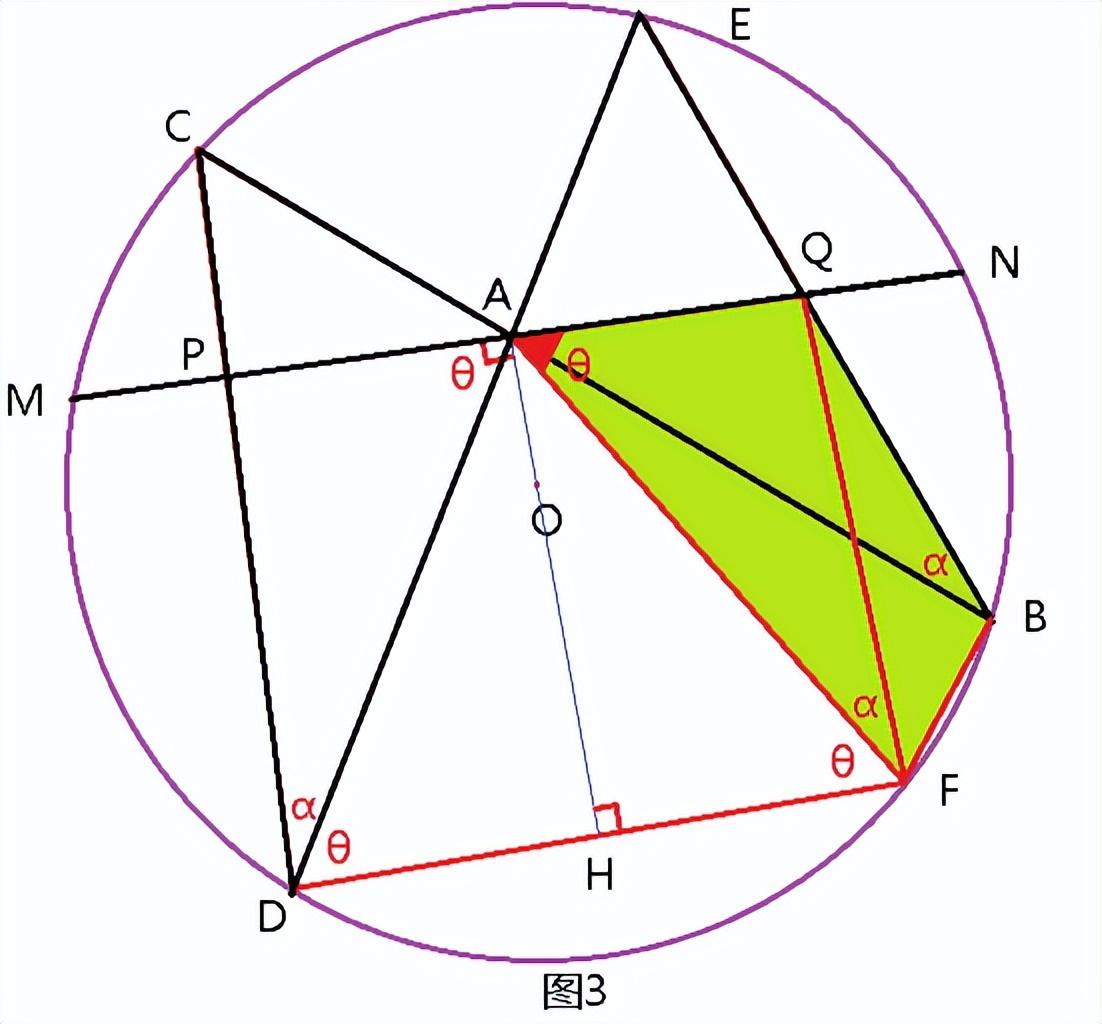
3.相似法
已知A为MN的中点,则AM=AN。
过点Q作CD的平行线交CB于F,交DE的延长线于G(图4),连接EF,易证G、E、F、B四点共圆。
根据相交弦定理则有:QG·QF= QE·QB,
PD·PC= PM·PN, QE·QB= QN·QM。
易证下列两组相似三角形:
△PAD∽△QAG,则PD/PA=QG/QA…………①;
△PAC∽△QAF,则PC/PA=QF/QA…………②,
将①x②得:
(PD·PC)/PA²=(QG·QF)/QA²,即
PA²/QA²=(PD·PC)/(QG·QF)
=(PM·PN)/(QE·QB)
=(PM·PN)/(QN·QM)
={(AM-PA)·(AN+PA)}/{(AN-QA)·(AM+QA)}
={(AM-PA)·(AM+PA)}/{(AM-QA)·(AM+QA)}
=(AM²-PA²)/(AM²-QA²),
即PA²/QA²=(AM²-PA²)/(AM²-QA²),根据比例性质:PA=QA。
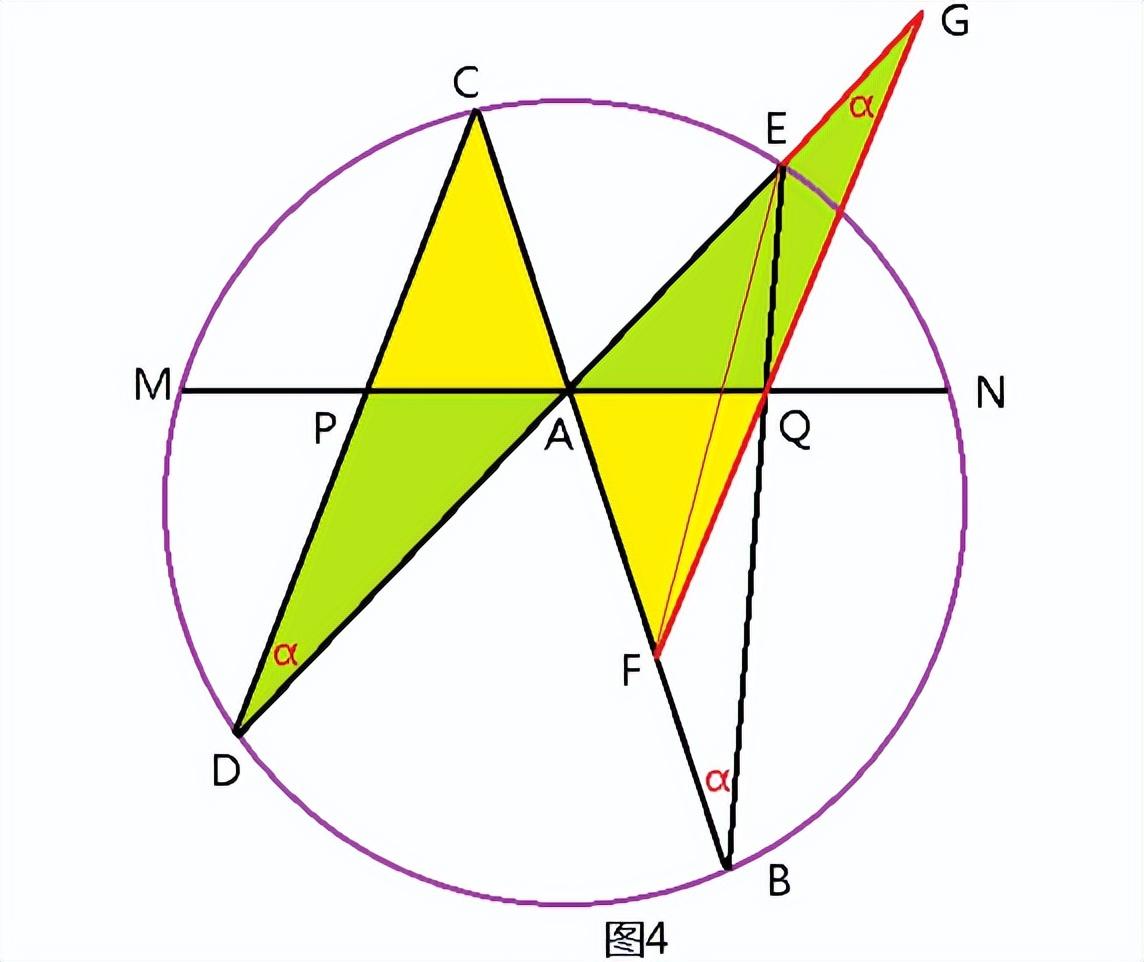
4.利用梅涅劳斯定理
延长DC、BE交于点F(图5)根据割线定理和相交弦定理有:FE·FB=FC·FD,
PC·PD=PM·PN,
QE·QB=QM·QN。
因△FPQ为DE所截,根据梅氏定理有:
FE/EQ·QA/AP·DP/DF=1;
同理,△FPQ为CB所截,
FC/CP·PA/AQ·BQ/BF=1,则
FE/EQ·QA/AP·DP/DF= FC/CP·PA/AQ·BQ/BF,即
FE·QA·DP·CP·AQ·BF=FC·PA·BQ·EQ·AP·DF,即FE·FB·QA ²·PC·PD= FC·FD·PA²·QE·QB,
即QA ²·PM·PN= PA²·QM·QN,
即PA²/QA²=(PM·PN)/( QM·QN),
剩余过程同相似法。

