圆的面积怎样算出来的（数学知识点总结-圆的面积）

1、圆的面积：圆所占平面的大小叫做圆的面积。通常用字母S表示面积，如S圆，S半圆等。

2、扇形：一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。顶点在圆心的角叫做圆心角。

3.圆面积公式的推导：

思想：用逐渐逼近的转化思想，化圆为方，化曲为直。

（1）把一个圆等分成偶数份的扇形。

（2）拼出的图形与圆的周长和半径的关系。

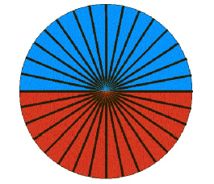
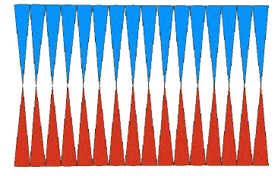
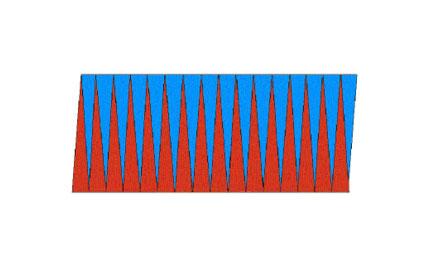
由图可知，拼成的图形近似一个长方形，近似长方形的长为圆的周长的一半πr，宽为圆的半径r，近似长方形的面积=πr×r，近似长方形的面积等于圆的面积，所以用S表示圆的面积，那么

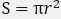
（3）把一个圆等分的扇形份数越多，拼成的图像越接近长方形。

4、环形面积：环形面积等于外圆的面积减去内圆的面积。

如：一个环形，外圆半径是R，内圆的半径是r。环的宽度=R-r

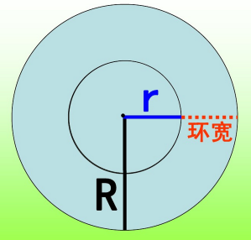
环形面积公式：

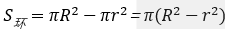
求环形面积的方法：首先想办法求出外圆半径和内圆半径，再代入公式计算。一步一步的来，这样不容易出现错误。

5、扇形的面积公式：

6、半径与直径、周长、面积的关系：一个圆，半径扩大或缩小多少倍，直径和周长也扩大或缩小相同的倍数，而面积扩大或缩小这个倍数的平方倍。

比如：有一个圆，半径扩大4倍，那么直径和周长扩大4倍，面积扩大16倍。

7、两个圆的半径比=直径比=周长比，而面积比=半径比的平方。

比如：两个圆的半径比为3:4，那么这两个圆的直径比和周长比都是3:4，而面积比是9:16。

8、任意一个正方形与它的内接圆的面积比都是一个固定值。

9、当长方形、正方形、圆的周长相等时，圆的面积最大，正方形次之，长方形面积最小。当它们面积相等时，长方形周长最长，正方形次之，圆周长最短。

10、确定操场跑道的起跑线：

（1）每条跑道的长度=两个半圆形跑道组合成圆的周长+两个直道的长度

（2）每条跑道直道的长度都相等，而各圆周长决定每条跑道的总长度。

（3）每相邻两个跑道相隔的距离：2×π×跑道的宽度

（4）当一个圆的半径增加a厘米时，它的周长就增加2πa厘米，当一个圆的直径增加a厘米时，它的周长就增加πa厘米。